
دستاوردهای مهم ریاضیات سال 2025 به انتخاب Scientific American
جهان علم مدرن، بیش از هر چیز، بر شانههای ریاضیات استوار است. با اینهمه، پیشرفتهای بنیادی ریاضی معمولاً کمتر از سایر شاخههای علم به رسانهها راه پیدا میکنند. پایان سال فرصتی است برای جبران این کمتوجهی.
در آستانه سال ۲۰۲۶، Scientific American نگاهی انداخته است به ده پیشرفت مهم ریاضی در سال گذشته؛ دستاوردهایی که از هندسه و توپولوژی تا نظریه اعداد و پیوند ریاضیات با فیزیک را در بر میگیرند. در ادامه، ترجمه و بازنویسی این گزارش را میخوانید.
۱) کشف یک شکل هندسی تازه

ریاضیدانان شکلی جدید به نام نوپرتهدرون را معرفی کردهاند؛ چندوجهیای با ۹۰ رأس، ۲۴۰ لبه و ۱۵۲ وجه. این ساختار پیچیده و باروک، یک حدس قدیمی هندسی را نقض میکند:
مهم نیست نوپرتهدرون را چگونه بچرخانید یا جابهجا کنید، هرگز نمیتواند از یک سوراخ مستقیم در نوپرتهدرونی کاملاً مشابه عبور کند.
۲) الگوهای پنهان در اعداد اول
اعداد اول—اعدادی که تنها بر خودشان و عدد یک بخشپذیرند—دهههاست ذهن ریاضیدانان را درگیر کردهاند. با بزرگتر شدن این اعداد، یافتن آنها دشوارتر میشود.
در سال گذشته، پژوهشگران مجموعهای از الگوهای آماری و ساختاری را شناسایی کردهاند که به توزیع اعداد اول مربوط میشوند؛ الگوهایی که ترکیبی از رفتار آشوبناک، تصادفی و حتی ساختارهای فراکتالی را نشان میدهند.
۳) گامی بهسوی «نظریه بزرگ یکپارچه ریاضیات»
یک تلاش عظیم پژوهشی—با مشارکت ۹ ریاضیدان و انتشار ۵ مقاله در مجموع نزدیک به ۱۰۰۰ صفحه—به اثبات حدس هندسی لنگلندز انجامیده است.

این حدس، ویژگیهای انواع مختلف سطوح ریمانی (ساختارهایی با مؤلفههای حقیقی و موهومی) را به هم پیوند میدهد. این نتیجه بخشی از پروژهای گستردهتر به نام برنامه لنگلندز است؛ برنامهای که در صورت تکمیل، میتواند به نوعی «نظریه بزرگ یکپارچه» در ریاضیات منجر شود.
۴) بازنگری در پیچیدگی گرهها
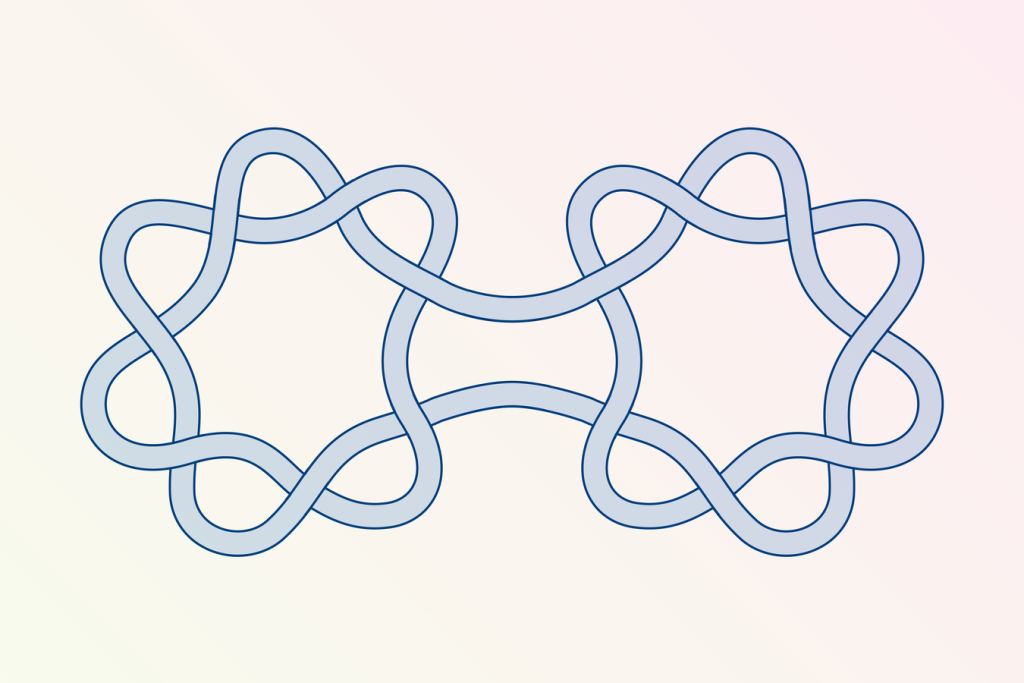
یک حدس دیرینه در توپولوژی میگفت اگر دو گره متفاوت را به هم متصل کنیم، پیچیدگی گره حاصل برابر با مجموع پیچیدگیهای آن دو خواهد بود.
اما کشف اخیر گرهای که سادهتر از مجموع اجزای تشکیلدهندهاش است، این فرض را رد کرده و نگاه تازهای به ریاضیات گرهها ارائه داده است.
۵) بازگشت فیبوناچی
دنباله فیبوناچی—که هر جمله آن حاصل جمع دو جمله پیشین است (۱، ۱، ۲، ۳، ۵، ۸، ۱۳ و …)—در طبیعت و ریاضیات حضوری گسترده دارد.
اکنون ریاضیدانان نشان دادهاند که این دنباله پاسخی برای نسخهای تغییریافته از یک مسئله کلاسیک به نام مسئله چوببرداری ارائه میدهد:
اگر تعدادی چوب با طولهای تصادفی بین صفر و یک داشته باشیم، احتمال اینکه هیچ سهتایی از آنها نتوانند یک مثلث بسازند، چقدر است؟
۶) شکار اعداد اول غولپیکر
بزرگترین عدد اول شناختهشده تاکنون، 2136,279,841 − 1 دارای 41,024,320 رقم است
با این حال، ریاضیدانان به این حد راضی نیستند. در سال گذشته، یک تیم پژوهشی رویکردی نو برای یافتن اعداد اول ناشناخته معرفی کرد که بر پایه پارتیشنها یا روشهای تجزیه عدد به مجموع اعداد دیگر استوار است.
۷) حل یک مسئله ۱۲۵ ساله هیلبرت
در سال ۱۹۰۰، دیوید هیلبرت فهرستی از مسائل بنیادین حلنشده ریاضیات را ارائه کرد. مسئله ششم او به دنبال کمینهکردن فرضهای ریاضی پشت قوانین فیزیک بود.
اکنون پژوهشگران اعلام کردهاند که یکی از زیرهدفهای این مسئله را به پایان رساندهاند: یکپارچهسازی سه نظریه فیزیکی برای توصیف حرکت سیالات. در صورت تأیید، این دستاورد گامی مهم بهسوی حل کامل مسئله ششم هیلبرت خواهد بود.
۸) از مثلث تا مربع
این پرسش قدیمی که یک مثلث را با چند قطعه میتوان به مربع تبدیل کرد، سرانجام پاسخ قطعیتری یافته است.
در سال ۱۹۰۲، راهحلی با چهار قطعه ارائه شده بود، اما کسی نتوانسته بود نشان دهد که با قطعات کمتر این کار ناممکن است.
امسال ریاضیدانان اثبات کردند که کمتر از چهار قطعه برای این تبدیل کافی نیست.

۹) مسئله جابهجایی مبل
هر کسی که تجربه اسبابکشی دارد، دشواری چرخاندن یک مبل بزرگ در راهرویی باریک را میشناسد.
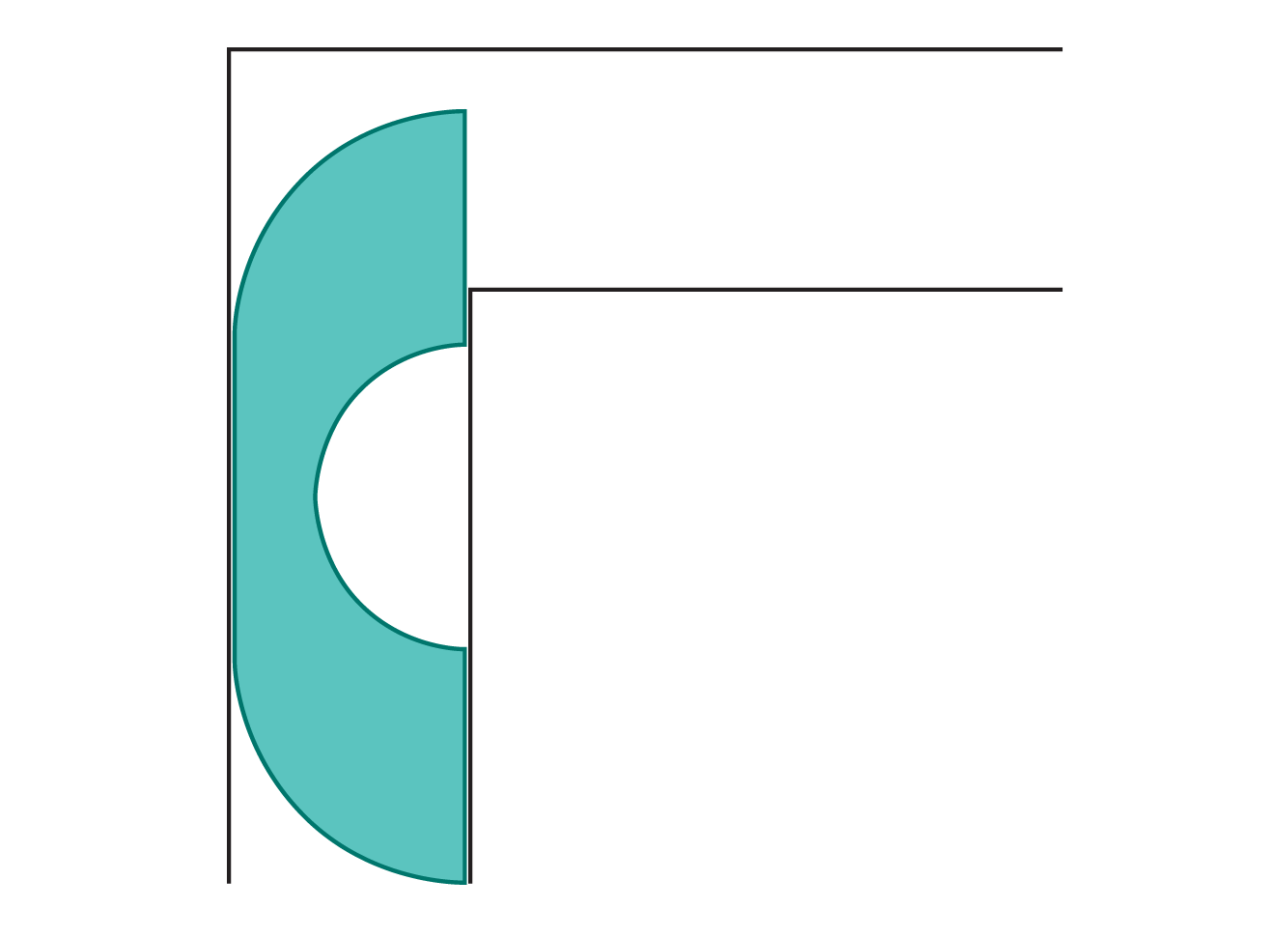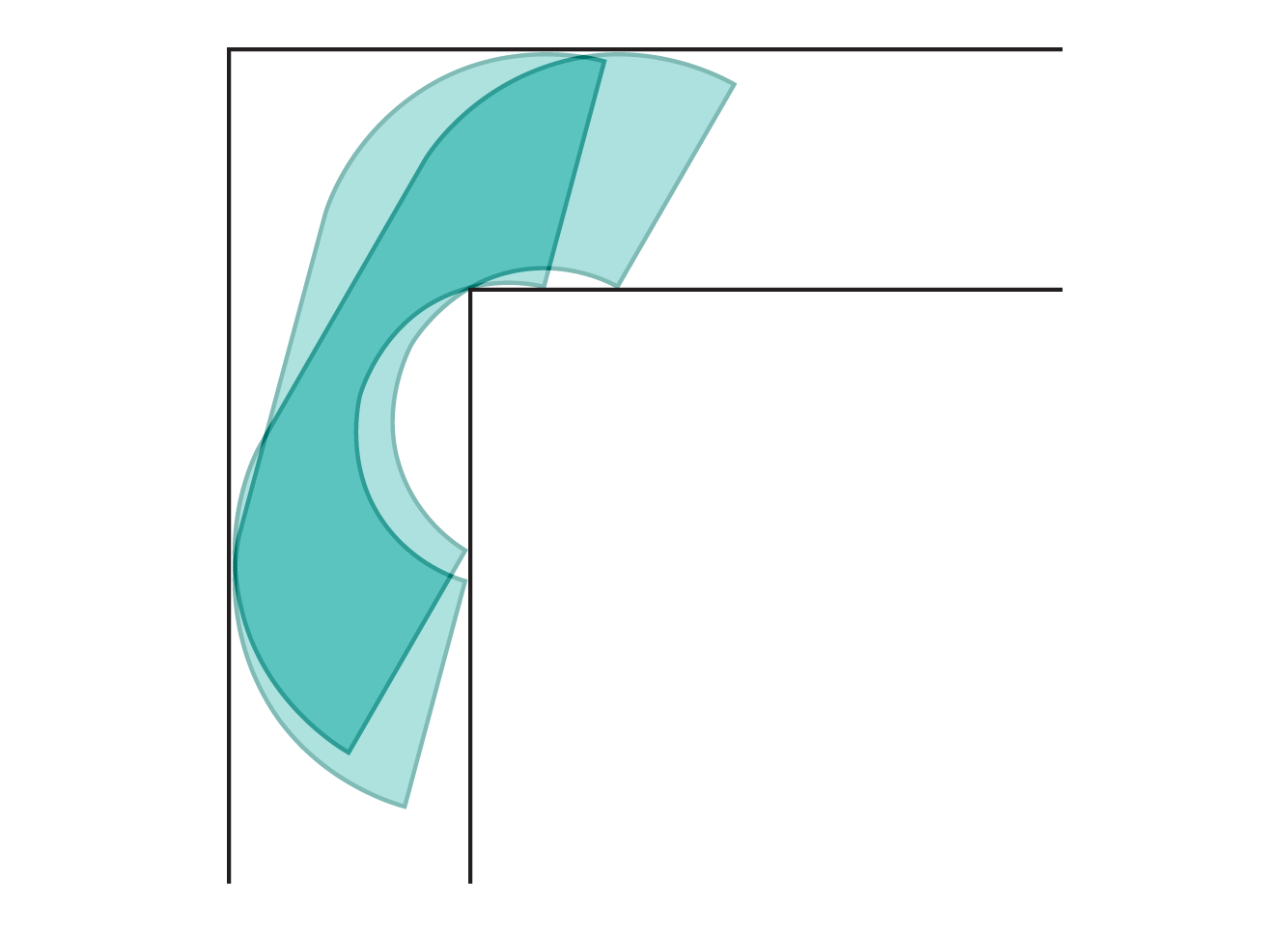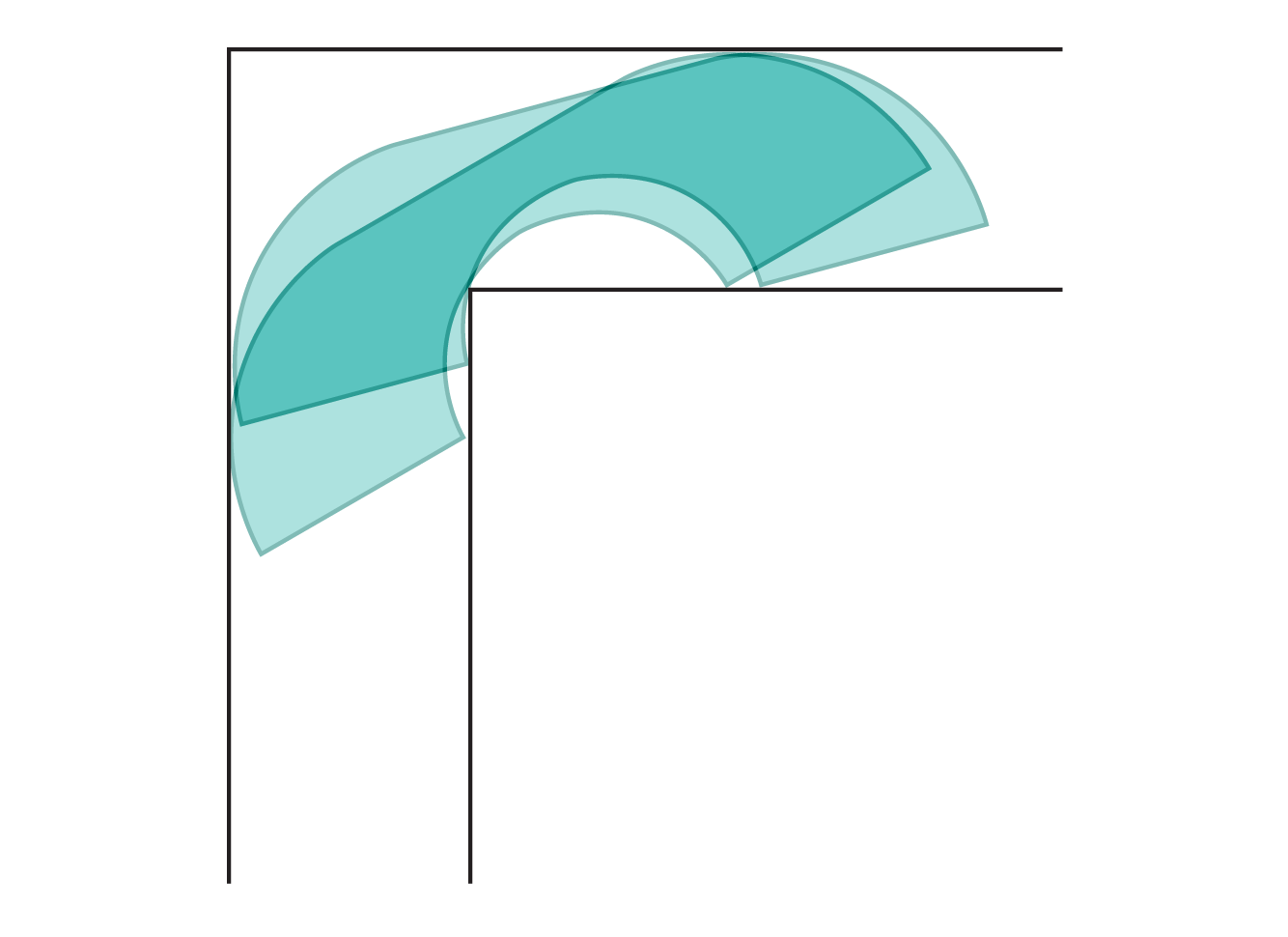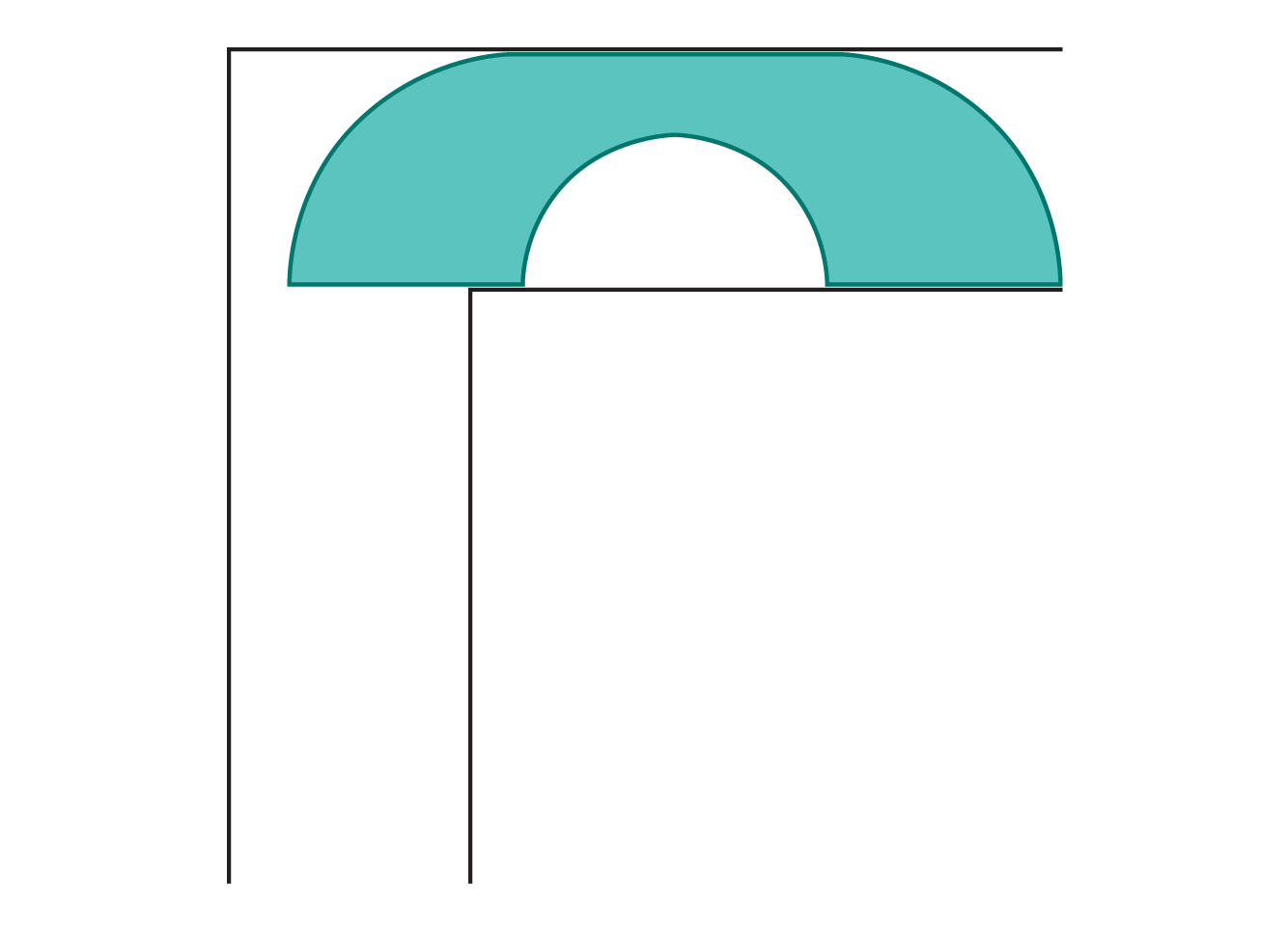
این مسئله حدود ۶۰ سال پیش بهطور رسمی وارد ریاضیات شد و به نام مسئله جابهجایی مبل شناخته میشود: بزرگترین شکلی که میتواند بدون گیرکردن از یک زاویه قائم عبور کند چیست؟
اکنون پژوهشگران پاسخی ریاضی برای این معما یافتهاند.
۱۰) تخمین تازهای از تعداد اعداد اول
در پیشرفتی دیگر در نظریه اعداد، روشی جدید برای تخمین تعداد اعداد اول در هر بازه عددی معرفی شده است.
این روش ابتدا اعدادی را که مضرب اعداد اول دیگرند حذف میکند و سپس بررسی میکند کدام اعداد بیش از یک بار کنار گذاشته شدهاند. پژوهشگران همچنین حدودی برای دقت چنین تخمینهایی تعیین کردهاند—حدودی که نشان میدهد رازهای بنیادین اعداد اول، دستکم فعلاً، همچنان حلنشده باقی میمانند.



